迁移学习(MEnsA)《MEnsA: Mix-up Ensemble Average for Unsupervised Multi Target Domain Adaptation on 3D Point Clouds》
2023-04-25 10:12:32 来源: 博客园
论文标题:MEnsA: Mix-up Ensemble Average for Unsupervised Multi Target Domain Adaptation on 3D Point Clouds论文作者:Ashish Sinha, Jonghyun Choi论文来源:2023CVPR论文地址:download论文代码:download视屏讲解:click1 前言
单目标域和多目标域
 (资料图片)
(资料图片)
单目标域和多目标域的差异:
3 方法3.1 整体框架3.2域 mixup 模块Mixup 模块:
$F_{i}^{m}=\lambda F_{s}+(1-\lambda) F_{T_{i}}\quad\quad(1)$
$L_{i}^{m}=\lambda L_{s}+(1-\lambda) L_{T_{i}} \quad\quad(2)$
线性差值的好处:
有助于创建一个连续域不变的潜在空间,使混合特征能够映射到源域和目标域的潜在空间之间的位置,这种连续的潜在空间对于跨多个域的域不变推理至关重要;作为一个有效的正则化器,帮助领域分类器 $D$ 在预测混合特征嵌入 $F_{mi}$ 的领域(源或目标) 的软分数方面有所提高;3.3 对比基线:【多目标域场景下】
形式:单源域和单目标域线性差值;问题:存在灾难性遗忘问题,只专注于学习源域和一个目标域之间的域不变特征,忽略了跨多个域的共享特征;本文:单源域 和 多目标域集成线性差值;
形式:$F_{m}^{M}=\frac{1}{n} \sum_{i=1}^{n} F_{i}^{m} \quad\quad(3)$;目的:旨在捕获跨多个域共享的域不变特征,减轻域间的冲突信息,提高泛化性;3.4 训练目标总损失:
$\mathcal{L}=\log \left(\sum\left(e^{\gamma\left(\mathcal{L}_{c l s}+\eta \mathcal{L}_{d c}+\zeta \mathcal{L}_{a d v}\right)}\right)\right) / \gamma \quad\quad(4)$
其中:
源域分类损失:$\mathcal{L}_{c l s} =\mathcal{L}_{C E}\left(C\left(F_{s}\right), y_{s}\right)\quad\quad(4)$
单源域单目标域鉴别损失:$\mathcal{L}_{d c} =\mathcal{L}_{C E}\left(D\left(F_{s}\right), L_{s}\right)+\mathcal{L}_{C E}\left(D\left(F_{T_{i}}, L_{T_{i}}\right)\right) \quad\quad(5)$
对抗损失:$\mathcal{L}_{a d v} =\lambda_{1} \mathcal{L}_{m m d}+\lambda_{2} \mathcal{L}_{d c}+\lambda_{3} \mathcal{L}_{\text {mixup }}\quad\quad(6)$
关于对抗损失:
MMD 损失:$\mathcal{L}_{m m d}=\mathcal{L}_{r b f}\left(C\left(F_{s}\right), F_{T_{i}}, \sigma\right) \quad\quad(7)$
线性差值域鉴别损失:$\mathcal{L}_{\text {mixup }}=\mathcal{L}_{C E}\left(D\left(F_{m}^{M}\right), L_{i}^{m}\right) \quad\quad(8)$
Note:
线性差值:
$F_{m}^{\text {factor }}=\lambda F_{s}+\sum_{i=1}^{n} \frac{1-\lambda}{n} F_{T_{i}}$
$F_{m}^{\text {concat }}=\left[\lambda F_{s}, \frac{1-\lambda}{n} F_{T_{1}}, \ldots, \frac{1-\lambda}{n} F_{T_{n}}\right]$
$.L_{m}^{\text {concat }}=[\lambda, 2 \frac{1-\lambda}{n}, \ldots, N \frac{1-\lambda}{n}]$
$F_{m}^{T}=\lambda F_{T_{1}}+(1-\lambda) F_{T_{2}}$
$L_{m}^{T}=\lambda L_{T_{1}}+(1-\lambda) L_{T_{2}}$
标签:
[责任编辑:]
猜你喜欢
- (2023-04-25)美股异动 | 宜人金科(YRD.US)涨超4.5% StockNews此前上调该股评级至“买入”
- (2023-04-25)微资讯!中国常驻联合国代表呼吁各国践行真正的多边主义
- (2023-04-25)今日热讯:记者探访复兴号智能动车组:增设多处“科技感”实用设施,4月26日起将首次亮相
- (2023-04-25)【全球新要闻】重磅持仓数据出炉!贵州茅台继续“稳坐”公募头号重仓股
- (2023-04-25)人手一碗的非遗疙瘩汤,竟透露黄河口美食文化新动向! 全球最资讯
- (2023-04-25)当前快报:DR奕瑞科:融资净买入349.22万元,融资余额5231.46万元(04-24)
- (2023-04-25)精彩看点:温州突发惨烈车祸!已身亡!
 绿了盐碱地 建成新粮仓(人民眼·盐碱地综合利用
绿了盐碱地 建成新粮仓(人民眼·盐碱地综合利用
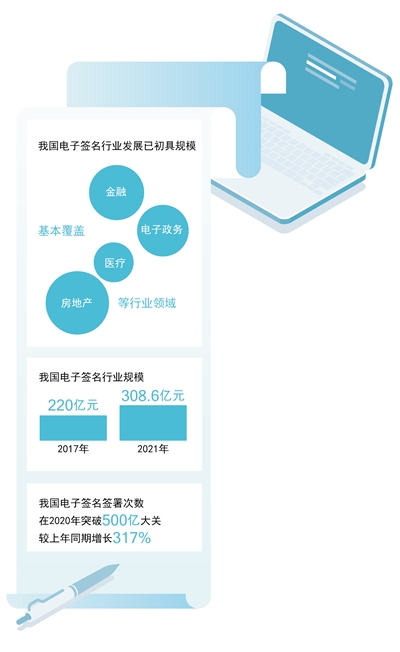 电子签名 方兴未艾(大数据观察·加快建设数字中
电子签名 方兴未艾(大数据观察·加快建设数字中